Effektstärken in der Psychotherapie

Sozial- und Verhaltenswissenschaftler stehen bei dem Versuch, ihre Forschungsergebnisse einem breiteren Publikum zu vermitteln und insbesondere Entscheidungsträgern, die darüber zu urteilen haben, ob bestimmte Maßnahmen ausreichend erfolgversprechend sind, um umgesetzt zu werden, vor einem Problem:
Effektstärken sind für Laien unanschaulich
Üblicherweise verwendet man in den Wissenschaften als Maßstab zur Beschreibung der in Frage stehenden Effekte Korrelationen, bzw. deren Quadrate (die Varianz, s.u.), um zu beschreiben, wie viel der parallel zur Durchführung einer Maßnahme beobachteten Veränderungen im Vergleich zu einer Kontrollgruppe retrospektiv durch eben dieselbe Maßnahme hätten prognostiziert werden können. Und die entsprechenden Werte, die man in den Sozial- und Verhaltenswissenschaften typischerweise erreicht, sind im Vergleich zu denen, die man in den „harten“ Naturwissenschaften erzielt, oft recht klein.
Auch kleine Effekte können bedeutsam sein
Wenn viel auf dem Spiel steht, Leben und Tod etwa, können aber auch kleine Effekte praktisch bedeutsam sein.
Von Jacob Cohen stammt eine Empfehlung, in den Verhaltenswissenschaften Effektstärken von ca. 0,2 oder 0,3 als klein, von 0,5 als mittelgroß und 0,8 als groß zu betrachten ([10], S.24 ff.). Dies ist nicht absolut, sondern immer in Relation zu dem, was in den Verhaltenswissenschaften typischerweise an Effekten erreicht bzw. beobachtet wird, zu verstehen. Die „Bedeutung“ ist darüber hinaus immer vom Kontext abhängig, z.B. ob man etwa über Leben und Tod spricht oder über relative Befindlichkeiten.
Die korrespondierenden Korrelationen und ihre Quadrate, die „erklärte“Varianz sind etwa:
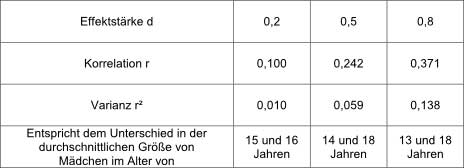
([10], S. 22-26, bei Punkt-biserieller Verteilung) (Varianz=Quadrat der Standardabweichung)
D.h. selbst ein recht „hoher“ Wert von d=0,8 erklärt nur ca. 13,8% der Variabilität der Ergebnisse (r²x100), die anderen 86,2% haben andere Ursachen. Es erwies sich als nicht immer ganz leicht, relativen Laien verständlich zu machen, dass auch solch ein Effekt mit d=0,8 (oder gar d=0,2 mit r²=0,01) praktisch bedeutungsvoll sein kann.
Versuche der Veranschaulichung
Daher werden zur besseren Veranschaulichung der Bedeutung der abstrakten Effektstärken oft verschiedene hypothetische Vergleichssituationen herangezogen und interpretiert. Alle diese Interpretationen haben ihre Vor- und Nachteile, weswegen im Folgenden einige gebräuchliche diskutiert werden sollen.
Man geht von zwei Gruppen bzw. Populationen aus. In einer wird die untersuchte Maßnahme durchgeführt (experimentelle Gruppe), in der anderen nicht (Kontrollgruppe). Die Veränderungen bei den Gruppenmitgliedern werden vor und nach der Maßnahme anhand kontinuierlich oder zumindest ordinal (der Größe nach sortierbarer) skalierter Messinstrumente, z.B. Persönlichkeitstests, beurteilt. Dabei wird von einer Normalverteilung der Ergebnisse ausgegangen.
Zur Erläuterung der Verhältnisse werden wieder die Ergebnisse der NIMH-Studie zur Depressionsbehandlung herangezogen (vgl. Teil 5 und 6).
Interpretation Nr.1
Häufig gibt man den Anteil der Patienten an, die besser als das typische Mitglied der Vergleichsgruppe abschneiden (dieses typische Mitglied wird durch den statistischen Mittelwert der Ergebnisse für die Vergleichsgruppe repräsentiert. Im unserem Beispiel ist die „keine Behandlung“-Gruppe die Vergleichsgruppe) (Cohen’s U3, [10] S.21; [4], S.45)
In der folgenden Graphik sieht man zunächst die Verteilungsdichten (je höher die Kurve, desto höher die Wahrscheinlichkeit, dass jemand in der Gruppe den zugehörigen HRSD-Punktewert hat) für die beste Therapie der NIMH-Studie (Interpersonale Therapie) im Vergleich mit der zugehörigen synthetischen „unbehandelten“ Gruppe (vgl. vorigen Beitrag). Der Mittelwert des Ergebnisses für die unbehandelte Gruppe (grün) wurde eingezeichnet (m=11,6), der für die Interpersonale Therapie (rot) war m=6,9 (s.Tabelle im vorigen Beitrag).
Durch die Behandlung verschiebt sich in unserem Beispiel die Kurve um die Effektstärke nach links (aus der grünen Kurve wird die rote Kurve).
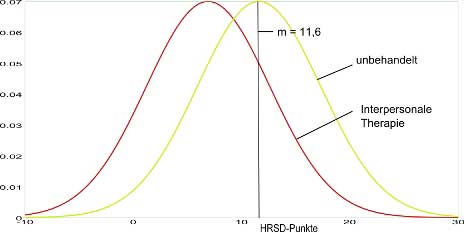
Bei einer Effektstärke von 0,82 sind ungefähr 79 von 100 Personen besser als der typische „keine Behandlung“-Fall. Das ist die Fläche unter der roten Kurve links vom eingezeichneten Mittelwert für die unbehandelte Gruppe im nächsten Bild (die gesamte Fläche unter jeder der Kurven ist immer gleich eins, was 100% entspricht).
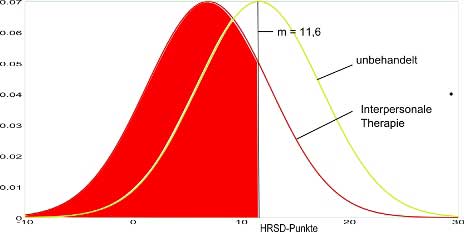
Doch selbst in der „keine Behandlung“-Gruppe schneiden im statistischen Mittel stets 50 von 100 Personen besser ab als der Durchschnittsfall in dieser Gruppe, das entspricht der grünen Fläche in der nächsten Graphik:
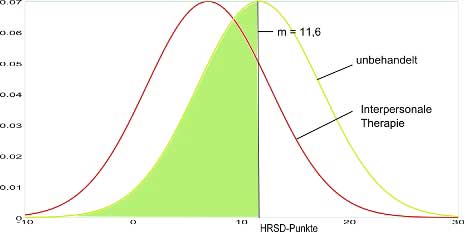
Eine Quote von 50 von 100 bedeutet soviel wie „kein Effekt“ bzw. „kein Unterschied“ zwischen den zu vergleichenden Gruppen. D.h. bei einer Quote der Verbesserung der Therapiegruppe von 50% gegenüber dem typischen „keine Behandlung“-Fall wäre kein Unterschied zwischen der Therapiegruppe und der „keine Behandlung“-Gruppe feststellbar.
Der Behandlungseffekt sieht anders aus
Aus diesem Grund ist die Interpretation Nr.1 von oben etwas irreführend. Sie erfordert für ein richtiges Verständnis die Kenntnis des zugrunde liegenden statistischen Modells, was bei Laien nicht immer vorausgesetzt werden kann.
Um den Effekt einer Behandlung zu ermitteln, muss man den Unterschied in den Erfolgsquoten der Populationen der behandelten und der unbehandelten Gruppe vergleichen. „Die Differenz zwischen den Erfolgen von EG [experimentelle Gruppe, hier die behandelte Gruppe] und KG [Kontrollgruppe, hier die unbehandelte Gruppe] beschreibt den Treatmenteffekt [Effekt der Behandlung] in Prozent.“[9].
Im vorliegenden Vergleich wird jedoch eine Population (die behandelte Gruppe) hinsichtlich der relativen Lage der Mitglieder derselben in Bezug auf den Mittelwert einer anderen Population (den von der unbehandelten Gruppe) mit sich selbst verglichen. Man vergleicht also gewissermaßen Äpfel mit Birnen.
Wie sieht das Bild nun aus, wenn man die beteiligten Populationen nach dem gleichen Kriterium, besser abzuschneiden als der Durchschnitt der unbehandelten Gruppe, miteinander vergleicht?
Das wäre dann auch tatsächlich ein direktes Korrelat der Effektstärke „d“, hier gemessen als Differenz zu den hypothetischen 50% nach dem Kriterium Erfolgreichen für die Kontrollgruppe (s.a. Cohen [10], S.10).
Ohne Behandlung schneiden 50% der Population der unbehandelten Gruppe besser ab als der Durchschnitt der unbehandelten Gruppe. Und mit Behandlung schneiden 79% der Population der behandelten Gruppe besser ab als der Durchschnitt der unbehandelten Gruppe.
Es haben also in der behandelten Gruppe 29% mehr den Durchschnitt der unbehandelten Gruppe übertroffen, als in der unbehandelten Gruppe. Das ist der der Effektstärke tatsächlich entsprechende Behandlungseffekt für das Vergleichskriterium, das Interpretation 1 zugrunde gelegt wurde.
Der Anteil der bei gleichem Kriterium dabei die Schwelle zur klinischen Relevanz (hier mit dem Kriterium d=0,5 angenommen, ergibt einen HRSD-Wert von 8,7) überscheitet (bzw. unterschreitet, niedrigere Werte sind hier ja besser), liegt bei ca. 63 von 100. Dieser Fall entspricht der roten Fläche in der nächsten Graphik.
Vergleicht man dies mit den 50 über dem Durchschnitt liegenden Personen aus der unbehandelten Gruppe (die grüne Fläche oben), so erhält man den Teil der 29 Personen der behandelten Gruppe, die besser als der Mittelwert der unbehandelten Gruppe sind und die außerdem in klinisch relevantem Maße besser als der Mittelwert der unbehandelten Gruppe sind. Das sind dann 13 Personen oder 13% der Population.
Zieht man dagegen zum Vergleich die geringere Anzahl der Personen heran, die sich auch ohne Behandlung in klinisch relevantem Maße gegenüber dem Kriterium verbessert haben, so findet man: 31 von 100 Personen aus der unbehandelten Gruppe sind in klinisch relevantem Ausmaß besser als der Mittelwert dieser Gruppe von 11,6 HRSD-Punkten (der Teil der roten Fläche in der nächsten Graphik, der unter der grünen Kurve liegt). In diesem Fall beträgt die Differenz also 63-31=32 Personen bzw. 32% der Gruppe.
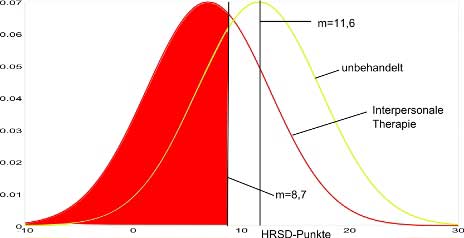
Dies zeigt die Bedeutung der Bezugsgrößen bei der Entwicklung derartiger hypothetischer Vergleiche und macht vielleicht auch deutlich, warum es lohnend sein kann, sich etwas detaillierter damit zu beschäftigen.
Im Prinzip müsste man derartige Vergleiche individuell je nach den bevorzugten Vergleichskriterien entwickeln. Das setzt aber eine genaue Kenntnis der statistischen Modelle sowie jeweils die Verfügbarkeit ausreichend detaillierter Daten voraus.
Ohne Handicap (vgl. Teil 6)
Die Berücksichtigung des Überzeugungseffektes (hier mit d = 0.47 angenommen, s. Teil 6) reduziert die Erfolgsquote für die „echte“ Therapie ungefähr von 29% auf 14% bzw. erhöht (alternativ) die für Placebogruppen (d=0,42 aus Lamberts Studie) von 16% auf ca. 31%. D.h. „echte“ Therapie und die „unbehandelte“ Gruppe schneiden ohne ein derartiges Handicap für die „unbehandelte“ Gruppe gleich gut ab.
Interpretation Nr.2
Eine andere Methode die Verhältnisse zu veranschaulichen, besteht darin, die Wahrscheinlichkeit zu vergleichen, dass ein zufällig aus der Psychotherapiegruppe ausgewählter Patient besser abschneidet, als ein zufällig ausgewähltes Mitglied einer unbehandelten Gruppe (CLES: Common Language Effect Size, [7]).
Bei einer Effektstärke von 0,82 bedeutet das: wählt man nacheinander nach dem Zufallsprinzip 100 Paare bestehend aus je einer Person aus der Therapie- und einer aus der unbehandelten Gruppe aus, so hat im Mittel in 72 Fällen die Person aus der Therapiegruppe einen besseren HRSD-Punktewert als die Person aus der unbehandelten Gruppe.
Wieder vergleicht man eine Population, die der zufällig gepaarten Personen aus unterschiedlichen Gruppen, mit sich selbst hinsichtlich des Mittelwerts des Ergebnisses für eine der beiden Gruppen.
Bei einer Effektstärke von 0 schneiden die Teilnehmer der Therapiegruppe immer noch in 50% der Fälle besser ab. Dasselbe Ergebnis bekommt man, wenn man die unbehandelte Gruppe mit sich selbst vergleicht.
Die Personen aus der Therapiegruppe liefern also nach dem Kriterium nur in 22 von 100 derartigen zufälligen Vergleichen zusätzlich ein besseres Ergebnis als die aus der unbehandelten Gruppe, als wenn auch die Therapiegruppe nicht behandelt worden wäre.
D.h. die Wahrscheinlichkeit bei diesem Vergleich besser als die unbehandelte Gruppe abzuschneiden hat sich durch die Therapie um 22% erhöht. Das ist der korrekte Behandlungseffekt.
Interpretation Nr.3a
Man kann auch die Überlappung der Gruppen mit und ohne Behandlung vergleichen.
Das nächste Bild zeigt den Anteil der Populationen der behandelten und der unbehandelten Leute, in dem sie sich HRSD-Punkte-mäßig überschneiden (die blaue Fläche in der nächsten Graphik). Für d=0,82 ergibt sich eine Überlappung von 68%.
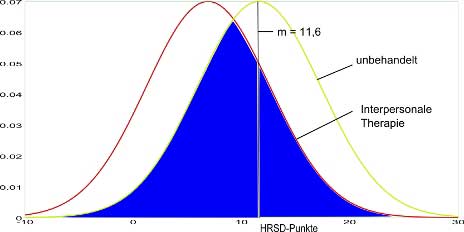
Die Differenz zu 100 ist der Anteil aus der behandelten Gruppe, denen es wegen der Behandlung besser geht als Leuten, die es HRSD-punktwertemäßig auch schon in der Population der unbehandelten Gruppe gab. Das sind offensichtlich 32 von 100 oder 32%. Das entspricht der roten Fläche in der nächsten Graphik.
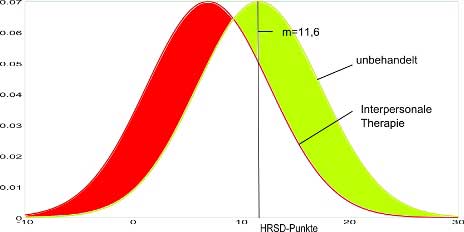
Berücksichtigt man auch den Anteil der unbehandelten Gruppe, denen es schlechter geht, als Vergleichspersonen aus der Therapiegruppe, so ändert sich am Ergebnis nichts:
Aus der behandelten Gruppe befinden sich nach den obigen Ergebnissen 32 von 100 Personen im nichtüberlappenden Bereich (das war der rote Bereich im letzten Bild). 68 Personen befinden sich im überlappenden (der blaue Bereich im vorhergehenden Bild).
Für die unbehandelte Gruppe befinden sich ebenfalls 32 von 100 Personen aus dieser Gruppe im nichtüberlappenden Bereich (das ist der grüne Bereich im letzten Bild). Im Überlappenden Bereich befinden sich wieder 68 Personen (blau im vorletzten Bild).
Insgesamt befinden sich also 64 Personen im nichtüberlappenden Bereich und 136 im überlappenden. Prozentual entspricht das wieder 32% und 68%, da es insgesamt 200 Personen waren.
Man beachte, dass die blaue Fläche von oben je 68 Personen aus beiden Gruppen entspricht und so bei der Veranschaulichung anhand der Flächen doppelt gezählt wurde.
Interpretation Nr.3b
In der Literatur findet man jedoch eine Methode, die den nicht überlappenden Bereich der beiden Gruppen zur Veranschaulichung heranzieht, aber nur den überlappenden Bereich von einer Gruppe.
Cohen (U1, [10] S.21) hat diese Veranschaulichungsmethode etabliert, der nicht die Zahlen aus den Populationen sondern einfach die Fläche unter den Kurven zugrunde gelegt wurde. Die Bezugsfläche ist dabei nicht die Summe der Flächen unter den beiden Glockenkurven (rot + grün + zweimal blau), sondern lediglich die sichtbare Fläche unter den beiden sich schneidenden Kurven (rot + grün + einmal blau). Dabei wird dann die blaue Fläche nur einmal gezählt.
Die „Erfolgsquote“ wird dadurch insbesondere im unteren Bereich höher berechnet. In unserem Fall wären das 64/(64+68)=0,48 statt 64/(64+2×68)=0,32 bzw. 48% statt 32%.
Bei d=0,2 zum Beispiel wären es 14,74% statt 7,96%. Fast das Doppelte.
Interpretation Nr.4
Eine weitere gebräuchliche Methode zur Veranschaulichung ist das Binomial Effect Size Display (BESD) [11].
Wieder nehmen unsere 200 Probanden an der Untersuchung teil und werden zu gleichen Teilen auf die behandelte und die unbehandelte Gruppe verteilt.
Nach Durchführung der Maßnahmen müssen 100 Probanden ein positives Ergebnis und 100 Probanden ein negatives Ergebnis erzielen. D.h. als mögliche Ergebnisse haben wir hier nur die beiden möglichen Werte positiv (erfolgreich) und negativ (kein Behandlungserfolg).
Damit diese relativen Verhältnisse beim Vergleich von Gruppen mit Individuen, die nach einem kontinuierlichen Punkteschema bewertet werden, erreicht werden, muß die Grenze zwischen Erfolg und Misserfolg genau in der Mitte zwischen den Mittelwerten für die beiden Gruppen liegen (das entspricht Cohen’s U2, [10] S. 21). Man beachte, dass dann das Kriterium für Erfolg bzw. Misserfolg von der relativen Lage der Gruppen zueinander (bzw. der Effektstärke) abhängt. Für unterschiedliche Effektstärken gelten i.a. unterschiedliche Maßstäbe für „Erfolg“ bzw. „Misserfolg“. Vergleicht man auf diese Weise die Auswirkungen verschiedener Effektstärken, so vergleicht man (mehr oder weniger) Äpfel mit (meist einigermaßen apfelförmigen) Birnen.
In unserem Fall läge dieses Kriterium bei der Hälfte von d=0,82, d.h. 0,41 bzw. 0,41×5,7=2,3 HRSD-Punkte vom Durchschnittswert der Therapiegruppe entfernt. Also bei 6,9+2,3=9,2 HRSD-Punkten. Das nächste Bild zeigt diese Verhältnisse: Rot entspricht „erfolgreich“ und blau „nicht erfolgreich“.
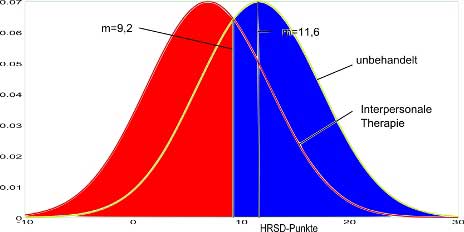
Dann wird gezählt, wie sich die erfolgreichen und erfolglosen Fälle auf die behandelte und die unbehandelte Gruppe verteilen. Die Differenz ist dann gleich dem Behandlungserfolg.
Das ganze kann man sich auch tabellarisch verdeutlichen:
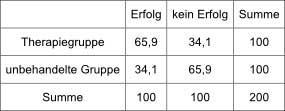
Bei der Effektstärke von 0,82 kommt man so zu einem Behandlungseffekt von ca. 31,8%.
Der Zusammenhang wird in der Literatur oft in tabellarischer Form angegeben. Dabei wird jedoch anscheinend immer der Korrelationskoeffizient für normal verteilte Gruppen (Punkt-biserielle Verteilung) mit dem für Kontingenztabellen der obigen Form mit dichotomen (zweiwertigen) abhängigen Variablen („Erfolg“ und kein „Erfolg“) gleichgesetzt. Das ist jedoch nicht ganz korrekt. Rosenthal und Rubin weisen in ihrer Originalarbeit [11], in der sie die BESD-Methode vorstellen, auf den Unterschied und entsprechende Umrechnungsfaktoren hin. Das führt dazu, dass in den gängigen Tabellen (z.B. [7], [12], aber auch das Beispiel bei Cohen [10] S. 533) offenbar generell zu hohe Werte angegeben werden. Im vorliegenden Fall findet man dort einen Behandlungseffekt von 38% statt der korrekten 31,8%.
Eine Tendenz?
Die Tendenz von Verzerrungen bei der Konstruktion von Vergleichswerten zur Veranschaulichung des Behandlungseffekts (s.a.o.) scheint systematisch zu Gunsten höherer Werte zu erfolgen.
Der „Verkaufseffekt“
Aber wer wollte sich auch schon einer Behandlung unterziehen, die je nach Betrachtungsweise und angelegtem Erfolgskriterium ca. 68-87% der Teilnehmer keinen Vorteil bringt? Oder aber die Kosten übernehmen?
Das Ansinnen würde zweifelsohne auf eine gewisse Zurückhaltung stoßen.
Da erinnert man sich als potentieller Kunde oder rechenschaftspflichtiger Kostenträger doch lieber an z.B. die Zahlen aus Lamberts Aussagen. Wie man dort sieht, erfahren 75% eine Verbesserung. Das ist deutlich ermutigender.
Aber es muss bedacht werden, dass es ja auch zahlreiche Fälle gibt, in denen der Effekt möglicherweise den Aufwand lohnt (im Mittel etwa 32 von 100, vgl. Interpretation 3a). Und wie in einem früheren Beitrag schon gezeigt wurde, spielt die Erwartungshaltung in der Psychotherapie eine entscheidende Rolle. Ein Patient, der davon ausgeht, dass die Therapie in ca. zwei Drittel der Fälle tatsächlich keinen Vorteil bringt, erwartet für sich selbst vermutlich auch nicht viel und bringt sich genau dadurch statistisch gesehen um den größten Teil des Effekts, den diese für ihn haben könnte. Ähnliches gilt für den Überzeugungseffekt durch den Therapeuten (s.o.), wenn dieser davon ausgeht, in zwei Dritteln der Fälle sowieso keinen Unterschied machen zu können.
Man könnte daher argumentieren, diese Umstände könnten vielleicht eine „optimistischere“ Sicht rechtfertigen.
Es bleiben Fragen
Es stellt sich aber letztlich die gleiche Frage wie bei der Beurteilung von Antidepressiva (Teil 3): Ist es nicht andererseits unmoralisch, die Patienten zu täuschen und ihnen vorzuspiegeln, eine Behandlung sei wirksamer, als sie es in Wahrheit ist?
Und noch wichtiger: lässt es sich rechtfertigen, den Menschen zu suggerieren, die den Behandlungen zugrunde liegenden Theorien würden durch derartige „Erfolge“ bestätigt, sie sprächen von realen kausalen Zusammenhängen anstatt von relativ schwachen statistischen Zusammenhängen, und auch das nur in Teilbereichen, während sie sich in anderen Bereichen im Widerspruch zur Erfahrung befinden [13]? – So können große Teile der allgemeinen Bevölkerung, aber insbesondere auch institutionelle Entscheidungsträger und Experten zu falschen Analysen, z.B. falscher Klassifikation von Erkrankungen, mit entsprechend negativen Konsequenzen für die Betroffenen, verleitet werden.
Autor: Karlheinz, CSN – Chemical Sensitivity Network, 17. August 2009
Teil I – VII
-
Teil: VI: Psychostudien unter der Lupe
Literatur:
[1] Elkin et. al. (1989). NIMH Treatment of Depression Collaborative Research Program: General Effectiveness of Treatment, Archives of General Psychiatry 46:971-82.
[2] National Institute for Clinical Excellence: Depression: management
of depression in primary and secondary care. Clinical practice guideline No 23. London: NICE; 2004.
[3] Lambert & Bergin (1994). The Effectiveness of Psychotherapy, in Handbook of Psychotherapy and Behavior Change, 4th ed., ed. Bergin & Garfield, 143-190, John Wiley & Sons.
[4] Reiband, Nadine (2006). Klient, Therapeut und das unbekannte Dritte, Carl-Auer Verlag.
[5] Luborsky et. al. (1997). The Psychotherapist Matters: Comparison of Outcomes across twenty-two Therapists and seven Patient’s Samples, Clinical Psychology: Science and Practice, 42, 602-11.
[6] Weinberger (1995). Common Factors aren’t so common: The common Factors Dilemma. Clinical Psychology: Science and Practice, 42, 45-69.
[7] Ledesma & Macbeth (2009). Computing Effect Size Measures with ViSta – The Visual Statistics System, Tutorials in Quantitative Methods for Psychology, Vol. 5(1), p. 25–34.
[8] Gibson, P. R., Elms, A. N. M., & Ruding, L. A. (2003). Perceived treatment efficacy for conventional and alternative therapies reported by persons with multiple chemical sensitivity. Environmental Health Perspectives, 111, 1498-1504.
[9] Seminar Bedeutung Effektstärken
[10] Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Hillsdale, NJ: Lawrence Earlbaum Associates.
[11] Rosenthal, R., & Rubin, D. B. (1982). A simple general purpose display of magnitude and experimental effect. Journal of Educational Psychology, 74, 166-169.
[12] Randolph & Edmondson (2005). Using the Binomial Effect Size Display (BESD) to Present the Magnitude of Effect Sizes to the Evaluation Audience. Practical Assessment Research & Evaluation, Vol 10, No 14.
[13] Mischel, Shoda, Ayduk (2007). Introduction to Personality: Toward an Integrative Science of the Person. Wiley.

Kommentar abgeben: